近日,清华大学丘成桐数学科学中心助理教授刘子文在量子纠错码研究方面取得一系列重要进展,其两篇合作论文于今年9月先后发表于物理学国际顶级期刊《物理评论快报》(Physical Review Letters,PRL)。
量子纠错是迈向容错量子计算进而实现量子优势的必由之路,其中的核心挑战在于如何设计能高效兼顾量子纠错性能与逻辑操作能力的量子纠错编码。刘子文的两项研究基于不同的数学思想和物理体系,为上述挑战开辟了新的研究范式,受到国内外学界的广泛关注。
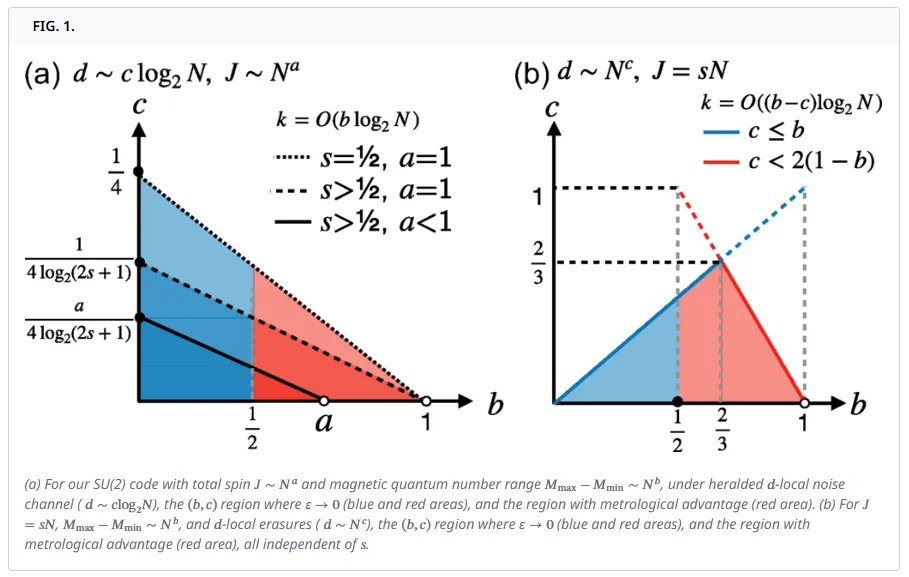
第一项研究题为《具有计量学纠缠优势的协变量子纠错码》(Covariant Quantum Error-Correcting Codes with Metrological Entanglement Advantage)。该研究首次提出并系统探讨了一类基于 SU(2) 对称性的协变近似量子纠错码,这类编码支持连续横向逻辑门操作,并在精密测量与传感等任务中展现出量子优势。该工作将“热力学码”的框架推广至一般自旋体系与不可约表示,由此展示了通过对称性构建近似量子纠错码的新途径。通过对这类新编码代数结构的严格分析,研究团队建立了误差修正能力的界限,并证明即使在存在噪声的情况下,这些纠错码仍可以保持量子 Fisher 信息超越经典极限,确保量子计量优势。这一成果不仅为量子纠错研究提供了新的视角,也为未来发展抗噪量子传感与精密测量开辟了新思路,从而为构建下一代高精度量子技术奠定了重要的理论基础。
论文链接
//journals.aps.org/prl/abstract/10.1103/dttc-ksdn
第二项研究题为《镶嵌码:通过几何旋转实现的编码量子逻辑门》(Tessellation Codes: Encoded Quantum Gates by Geometric Rotation)。该研究建立了另一类基于几何的新型量子纠错编码框架——“镶嵌码”(tessellation codes)。与传统方法不同,镶嵌码框架使得量子逻辑操作可直接通过几何旋转来实现,不仅为逻辑量子计算提供了基于几何操作的全新路径,更揭示了量子编码理论与数学之间内在的深刻联系。
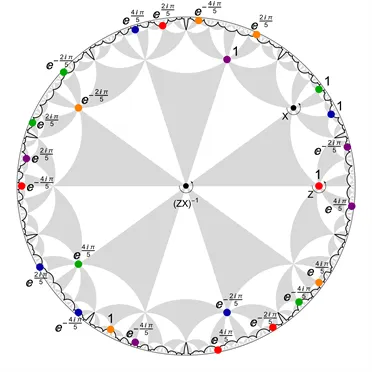
图:镶嵌码及其上几何旋转量子逻辑门示意图
具体而言,该研究系统建立了镶嵌码在不同几何上的普适构造的理论,并结合群论与表示论,展示其误差纠正能力。该研究还详细探讨了如何在球面、平面和双曲面等不同曲率的二维曲面上,利用不同正则镶嵌的对称群来实现量子信息的编码与逻辑门操作。论文还给出了多类具体示例,展示了该框架下可实现多种逻辑群和相应的逻辑门集合。未来,该方向期望拓宽容错量子计算的实验方案,并推动量子计算与数学几何方法的进一步交叉融合。
论文链接
//link.aps.org/doi/10.1103/tljb-f7tt
清华新闻网链接
//www.venetian777.com/info/1175/121667.htm
这两项连续发表的工作,从不同数学视角推进了量子纠错码的理论前沿,彰显了数学理论与量子信息科学深度交叉所产生的创新活力,为容错量子计算的未来发展提供了重要的理论支撑。

刘子文,现任清华大学丘成桐数学科学中心助理教授。美国麻省理工学院物理学博士,曾任圆周理论物理研究所资深博士后研究员。主要研究领域为量子信息与计算理论及其与数学、物理学的交叉研究,在Nature Physics、PRX Quantum、PRL等权威学术期刊发表论文数十篇。